Projects supervised at Purdue
Fall 2022
Project: Numerical method for Hotspots problem
Undergraduate Students: Zijie Zhang
Project description: We studied the numerical method for looking for hotspots in a domain that was introduced by Kleefeld. This project consists both theoretical study and programming practice.
Jan. 2021-May 2022
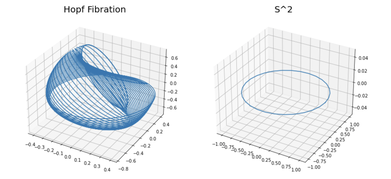
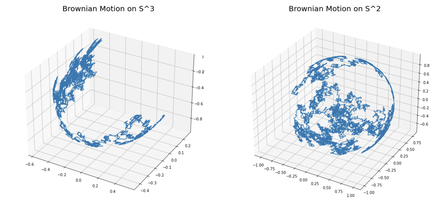
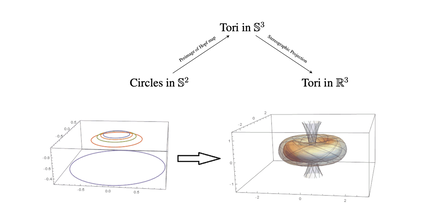
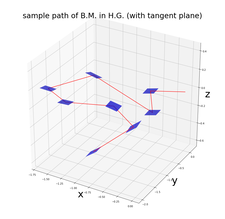
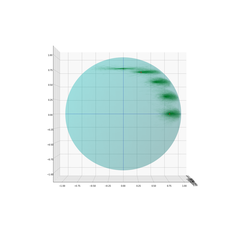
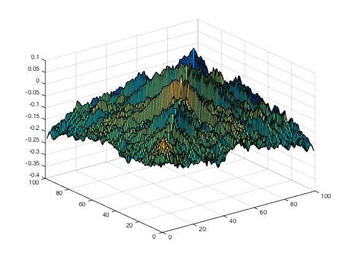
Project: Visualization of Brownian motion on sub-Riemannian model spaces
Undergraduate Students: Zijin Liu
Project description: This project includes visualization of horizontal Brownian motion processes on both SU(2) (the spherical model) and SL(2,R) (the hyperbolic model). It consists
- Theoretical study of sub-Riemannian manifolds, in particular the Hopf-fibration and its hyperbolic counterpart
- Understand Brownian motion as limiting process of a random walk.
- Use MatLab to visualize SU(2) and SL(2,R) as fibration structures.
- Use MatLab to visualize Brownian motions on SU(2) and SL(2,R).
- Use MatLab to visualize SU(2) and SL(2,R) as fibration structures.
Fall 2018
Project: Brownian motion on SU(2).
Undergraduate Students: Junyao Wu
Project description: This project focuses on
- Theoretical study of sub-Riemannian manifolds, in particular the Hopf-fibration.
- Understand Brownian motion as limiting process of a random walk.
Projects supervised at UIUC
Spring 2018
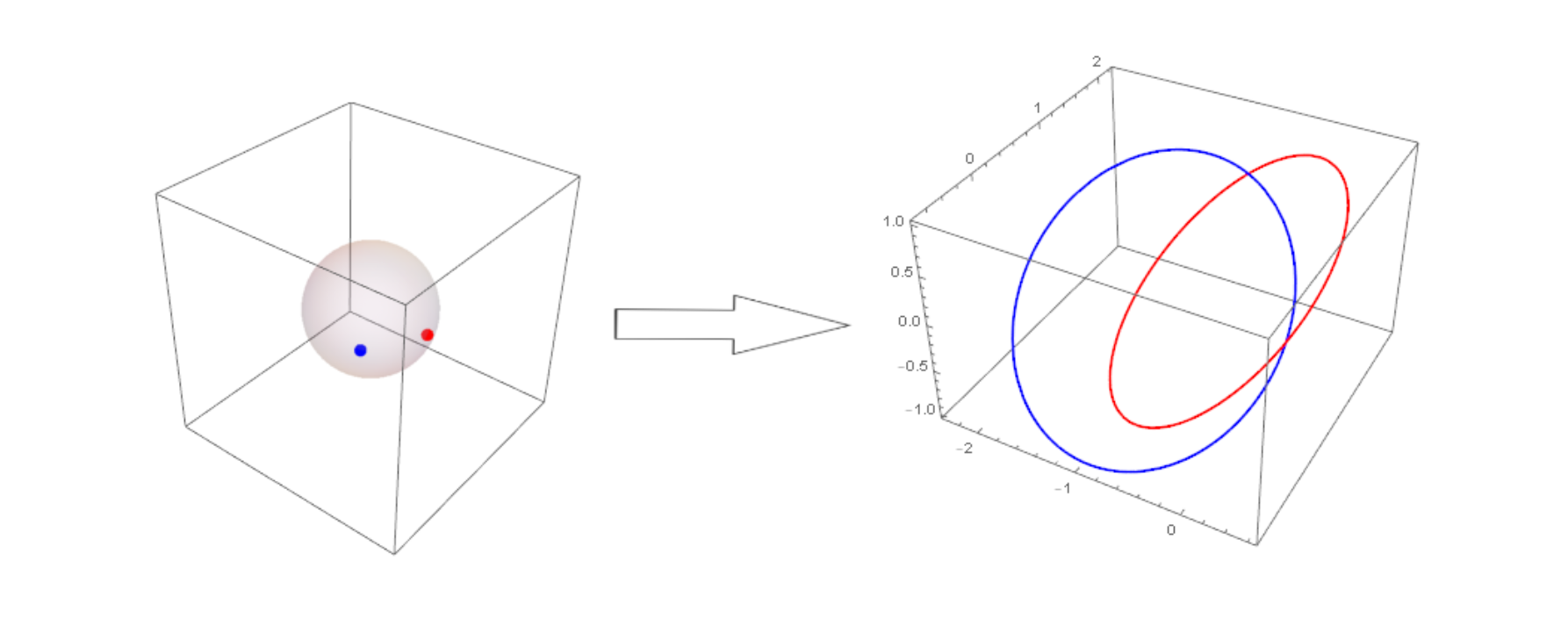
Project I: Brownian Motion on a CR Sphere
Graduate RA: Derek Jung
Undergraduate Students: Tianyu Hou, Hanyu Lu, Courtney Seckman, Mingchao Zhang
Project description: This project focuses on visualize Brownian motion on the CR sphere, which is the 3-sphere equipped with a sub-Riemannian structure. The first step is to visualize the Hopf fibration on the CR sphere. The second step is to use the visualization from the first step to simulate Brownian motion on the CR sphere.
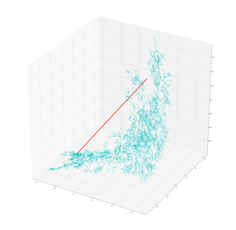
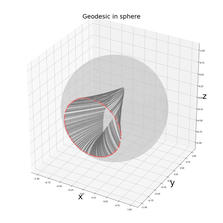
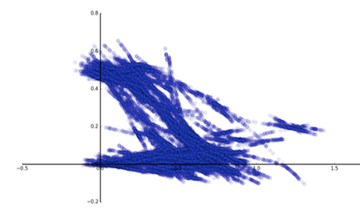
Project II: Degenerate Diffusions on the Heisenberg group
Graduate RA: Derek Kielty
Undergraduate Students: Andrew Jiang, Yirui Luo, Roger Qiu, Congwei Yang
Project description: This project aims to explore the degenerate structure of the Heisenberg group using by simulating Brownian movement. This include
- Simulation of sub-Riemannian Brownian bridge in the Heisenberg group.
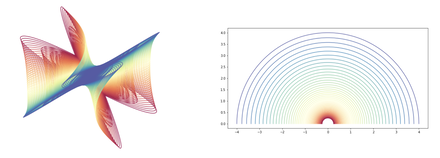
- Using the idea of Large deviation Principle to visualize the sub-Riemannian geodesics (the most energy economical paths) in the Heisenberg group.
- Visualize the characteristic point of a sphere in the Heisenberg group by simulating the exiting path of sub-Riemannian diffusions from the sphere.
Summer 2016
Project: Brownian sheet and Brownian motion on the Heisenberg group
Undergraduate Student: Zhe Hu
Project description: Visualization of Brownian sheet
Project: Brownian sheet and Brownian motion on the Heisenberg group
Undergraduate Student: Zhe Hu
Project description: Visualization of Brownian sheet
Spring 2016
Project: Brownian motion and diffusion processes [Poster]
Graduate RA: Derek Jung, Yunchao Qi
Undergraduate Students: Lucas M. Capoia, John A. Haug, Zhe Hu, Zhaopeng Liu
Project description: This project studies degenerate diffusions both theoretically and numerically. This include
- Develop algorithms for simulating small time (large deviation) behavior of degenerate diffusions which reveals the best paths (geodesics).
- Simulate for the group SE(2) (model for parallel parking)
- Simulate for the Kolmogorov process (strong degenerate process) in the plane and observe the fact its best paths are time dependent.
All pictures in this page are generated by students in each project.