Heat kernel analysis has been an useful tool to extract geometric information that is encoded in the Laplacian. A classic approach is to study the small time asymptotic behavior of the heat kernel. For instance, the celebrated Varadhan's estimate \[\lim_{t\to0} 2t\log p_t(x,y)=-d(x,y)^2,\]
provides the relation between the heat kernel and the Riemannian distance d(x,y) on a complete Riemannian manifold. Intuitively speaking, this suggests that the most likely chosen paths of Brownian motion on a Riemannian manifold travel from x to y within an extremely short time, concentrate around the most economic path -the geodesic connecting x and y.
The simplest example is the heat kernel on Euclidean space. We have
\[ \lim_{t\to0}2t\log p_t(x,y)=\lim_{t\to0}2t\log\left( \frac{1}{(2\pi t)^{n/2}}e^{-\frac{|x-y|^2}{2t}} \right)=-|x-y|^2.\]
This result was successfully generalized to subelliptic heat kernels, namely, transition densities of diffusion processes on sub-Riemannian manifolds by Leandre. A simple example is the Brownian motion on Heisenberg group.
My research concerns a more degenerate case-the transition densities of weak-Hormander-type diffusion processes, namely the Hormander's bracket generating condition is fulfilled by using the drift term. The simplest example is the Kolmogorov process.
\[
\left(w_t, \int_0^t w_sds\right)\quad \mbox{with generator } L=\frac{1}{2}\frac{\partial^2}{\partial x^2}+x\frac{\partial}{\partial y}
\]
Its transition density from point x arriving to y at time t is given by
\[
p_t(x,y)=\frac{\sqrt{12}}{2\pi t^2}\exp\bigg\{-\frac{2}{t}(y_1-x_1)^2+\frac{6}{t^2}(y_1-x_1)(y_2-x_2-tx_1)-\frac{6}{t^3}(y_2-x_2-tx_1)^2\bigg\}.
\]
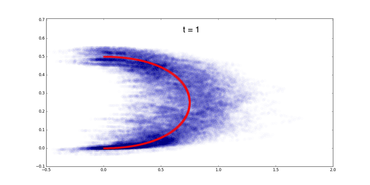
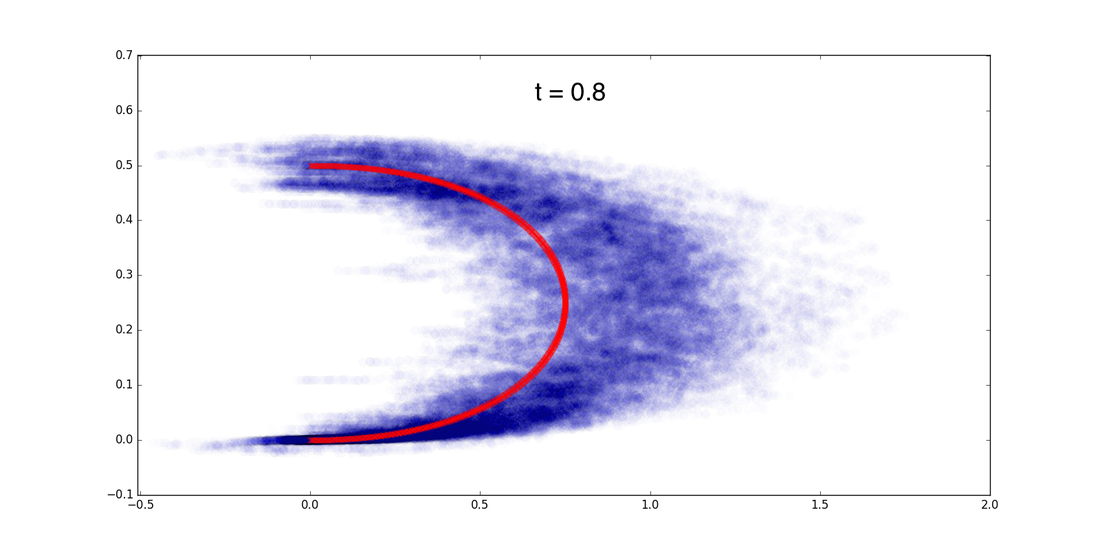
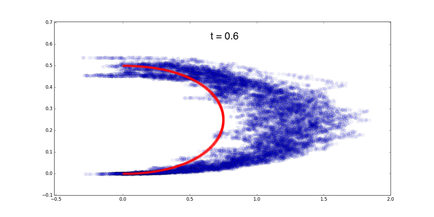
The energy minimizing path is now time dependent. As we can see from the simulation below, its ``optimal path'' diverges away as t decrease to 0.
provides the relation between the heat kernel and the Riemannian distance d(x,y) on a complete Riemannian manifold. Intuitively speaking, this suggests that the most likely chosen paths of Brownian motion on a Riemannian manifold travel from x to y within an extremely short time, concentrate around the most economic path -the geodesic connecting x and y.
The simplest example is the heat kernel on Euclidean space. We have
\[ \lim_{t\to0}2t\log p_t(x,y)=\lim_{t\to0}2t\log\left( \frac{1}{(2\pi t)^{n/2}}e^{-\frac{|x-y|^2}{2t}} \right)=-|x-y|^2.\]
This result was successfully generalized to subelliptic heat kernels, namely, transition densities of diffusion processes on sub-Riemannian manifolds by Leandre. A simple example is the Brownian motion on Heisenberg group.
My research concerns a more degenerate case-the transition densities of weak-Hormander-type diffusion processes, namely the Hormander's bracket generating condition is fulfilled by using the drift term. The simplest example is the Kolmogorov process.
\[
\left(w_t, \int_0^t w_sds\right)\quad \mbox{with generator } L=\frac{1}{2}\frac{\partial^2}{\partial x^2}+x\frac{\partial}{\partial y}
\]
Its transition density from point x arriving to y at time t is given by
\[
p_t(x,y)=\frac{\sqrt{12}}{2\pi t^2}\exp\bigg\{-\frac{2}{t}(y_1-x_1)^2+\frac{6}{t^2}(y_1-x_1)(y_2-x_2-tx_1)-\frac{6}{t^3}(y_2-x_2-tx_1)^2\bigg\}.
\]
The energy minimizing path is now time dependent. As we can see from the simulation below, its ``optimal path'' diverges away as t decrease to 0.
In an on-going project with Ben Arous, we obtain large deviation estimates for weak-Hormander type diffusions that can be lifted to a nilpotent group. There exist a sequence of positive rational number
\[
1=\alpha_1<\cdots<\alpha_{\ell}<\infty \quad \mbox{and rate functions } I^{+}_{\alpha_k}(\cdot)\ \mbox{and } I^{-}_{\alpha_k}(\cdot)
\]
such that for any open set G and closed set C of continuous path equipped with uniform norm, we have
\[\liminf_{t\to0}t^{\alpha_k}\log \mathbb{P}(x_t\in G)\ge -I^-_{\alpha_k}(G)\]
and
\[
\limsup_{t\to0}t^{\alpha_k}\log\mathbb{P}(x_t\in C)\le -I^+_{\alpha_k}(C)
\]
\[
1=\alpha_1<\cdots<\alpha_{\ell}<\infty \quad \mbox{and rate functions } I^{+}_{\alpha_k}(\cdot)\ \mbox{and } I^{-}_{\alpha_k}(\cdot)
\]
such that for any open set G and closed set C of continuous path equipped with uniform norm, we have
\[\liminf_{t\to0}t^{\alpha_k}\log \mathbb{P}(x_t\in G)\ge -I^-_{\alpha_k}(G)\]
and
\[
\limsup_{t\to0}t^{\alpha_k}\log\mathbb{P}(x_t\in C)\le -I^+_{\alpha_k}(C)
\]