I am interested in the Brownian motion processes on sub-Riemannian model spaces, and the explicit expressions for their transition densities. A classic example is the Brownian motion on Heisenberg group, which is given by
\[(B_t, \beta_t, \int_0^t B_sd\beta_s-\beta_sdB_s) \]
The last coordinate process is the stochastic process that is of twice the area swept by the planar Brownian motion, which is also known as the Levy area process. A sample path of this process is shown in the figure below.
\[(B_t, \beta_t, \int_0^t B_sd\beta_s-\beta_sdB_s) \]
The last coordinate process is the stochastic process that is of twice the area swept by the planar Brownian motion, which is also known as the Levy area process. A sample path of this process is shown in the figure below.
As Heisenberg group appears as a flat model for the sub-Riemannian geometry, the Cauchy- Riemann sphere and the anti-de Sitter space are known to be the models for positively and negatively curved sub-Riemannian manifolds. My research interests are to study the canonically associated Brownian motion processes on these models. The key is to notice the fibration structure of these two spaces.
\[\mathbf{U}(1)\to\mathbb{S}^{2n+1}\to\mathbb{CP}^n,\quad \mathbf{U}(1)\to\mathbb{H}^{2n+1}\to\mathbb{CH}^n \]
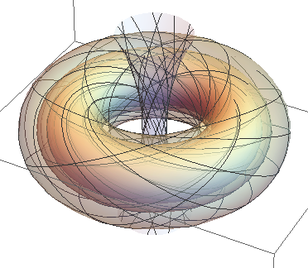
In the joint work with Baudoin, we construct Brownian motion processes on both of the above spaces, by lifting the Brownian motion on the n-dimensional complex projective space (complex hyperbolic space) through the Hopf fibration (hyperbolic fibration). The second figure above illustrate the Hopf fibration of the 3-sphere.
For instance, if we denote by w(t) the Brownian motion on the complex project space, then the stochastic area process is given by
\[
\theta(t)=\frac{i}{2}\sum_{j=1}^n \int_0^t \frac{w_j(s) d\overline{w_j}(s)-\overline{w_j}(s) dw_j(s)}{1+|w(s)|^2},
\]
and Brownian motion on the CR sphere is given by
\[
X_t=\frac{e^{-i\theta(t)} }{\sqrt{1+|w(t)|^2}} \left( w(t),1\right), \quad t \ge 0
\]
Moreover, we are able to characterize the law of the stochastic area process
\[
\mathbb{E}\left(e^{i \lambda \theta(t)}\right)=e^{-n | \lambda | t}\int_0^{\pi /2} \frac{q_t^{n-1,| \lambda |}(0,r)}{(\cos r)^{| \lambda|}} dr.
\]
and obtain its limiting behavior as time goes to infinity
\[\frac{\theta(t)}{t} \to \mbox{Cauchy distribution with parameter }n\]
\[\mathbf{U}(1)\to\mathbb{S}^{2n+1}\to\mathbb{CP}^n,\quad \mathbf{U}(1)\to\mathbb{H}^{2n+1}\to\mathbb{CH}^n \]
In the joint work with Baudoin, we construct Brownian motion processes on both of the above spaces, by lifting the Brownian motion on the n-dimensional complex projective space (complex hyperbolic space) through the Hopf fibration (hyperbolic fibration). The second figure above illustrate the Hopf fibration of the 3-sphere.
For instance, if we denote by w(t) the Brownian motion on the complex project space, then the stochastic area process is given by
\[
\theta(t)=\frac{i}{2}\sum_{j=1}^n \int_0^t \frac{w_j(s) d\overline{w_j}(s)-\overline{w_j}(s) dw_j(s)}{1+|w(s)|^2},
\]
and Brownian motion on the CR sphere is given by
\[
X_t=\frac{e^{-i\theta(t)} }{\sqrt{1+|w(t)|^2}} \left( w(t),1\right), \quad t \ge 0
\]
Moreover, we are able to characterize the law of the stochastic area process
\[
\mathbb{E}\left(e^{i \lambda \theta(t)}\right)=e^{-n | \lambda | t}\int_0^{\pi /2} \frac{q_t^{n-1,| \lambda |}(0,r)}{(\cos r)^{| \lambda|}} dr.
\]
and obtain its limiting behavior as time goes to infinity
\[\frac{\theta(t)}{t} \to \mbox{Cauchy distribution with parameter }n\]